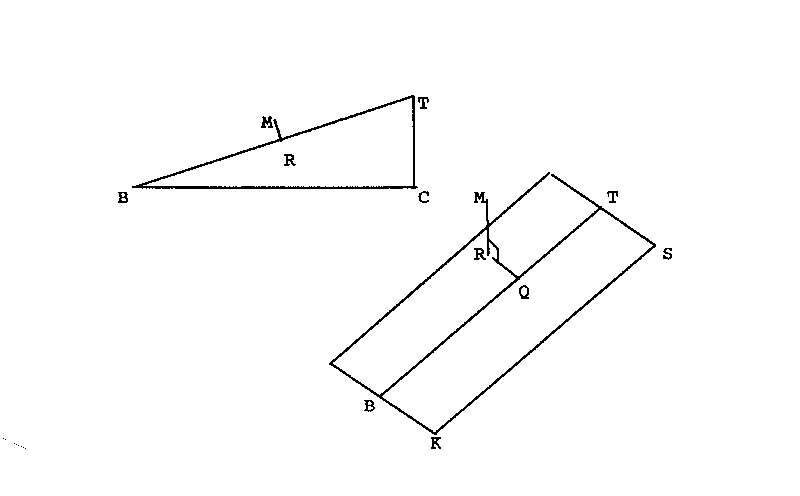

The top diagram the bearing in cross section and the bottom diagram shows an isometric view of the bearing. The main elements of the two diagrams are listed below.
BT is the axis of the bearing.
BK & TS are parallel, horizontal and at right angles to
BT.
M is the point whose position in relation to BT is required.
These co-ords are (QR, BQ, RM), equivalent to (x,y,z)
In order to solve this problem using vectors, I will introduce another vector fact.
Let a pyramid have an apex of A and a base of BDC.
Let AB = (bl,b2,b3)
Let AC = (cl,c2,c3)
Let AD = (dl,d2,d3)
Then the volume of the pyramid = det [[bl,b2,b3]
[cl,c2,c3]
[dl.d2.d3]]
6
(The above shows the formula is in HP 48 notation)
In 48 terms you would have to form the vectors first, place then one at a time on the stack, then create a matrix. The command is ROW~. (See page 14-3 in the user manual; the DET command is found on page 14-9
Also, volume of a pyramid is = (area of base)*(height of apex)
3
Now back at our diagram; if we form a pyramid with a base of BTS and a apex of M; we can utilise the above facts.
First by calculating the volume of the pyramid MTSB by using the vectors from the apex (M) to base points BTS. Let volume = V
Then calculating the area of the base. Area = A = BT*T
2
(Area could also be calculated by using @)
Let h = MR
Then h = 3*V
A
Now as stated before RQ can easily be found by conventional methods. All that remains to be found is BQ. This can easily be found by Pythagoras.
distance (slant) BM = ABS(vector BM)
Then we have BQ2 = BM2 - RQ2 - RM2
You have to be careful of signs when calculating in the above context. How vectors are chosen will determine the sign of the volume. It is best to choose the vectors in the same manner each time. Try to make a positive volume for a point above the axis BT. This will result in a positive distance MR. Also make sure that the base area is always positive.
The above derivation of BQ will always give a positive result. In the mill context this is obviously correct. For other applications this may not be the case. You could set some test to determine the sign. Perhaps the @ product could be used.
As with most Surveying problems there are usually a few different ways of solving the problem. Using matrix transformation is another way. One day I might write that method up also.
There was one other complication involved with the mill bearing. At the bottom end the exact centre of the bearing could not be located. Three points on the outside of the bearing were picked up. The bearing being round three points should be enough to fix the centre.
However because the circle picked up is not in either the horizontal or vertical planes; the centre cannot be calculated in the normal way. If you project the circle onto the horizontal plane you will get an ellipse. Same applies to the vertical plane.
The problem can be solved using vectors. I will leave this as an exercise for the reader. If you really want to know send me an e-mail and I will give you the answer.
FINAL APPLICATION.
(Final in the sense that I wish to finish off the tutorial. There are probably many more applications.
It must be obvious by now that vectors can be used in the ordinary close situation. A Surveying close is really the addition of vectors. The HP 48 is an ideal platform for this type of calculation.
What is probably not immediately obvious is the application of vectors to the calculation of a bowditch adjusted area. ie. calculating the bowditch adjusted area without doing the actual bowditch adjustment.
You will recall that A@B = ab sin(t).
Therefore the area enclosed by the two vectors A & B = A@B
2
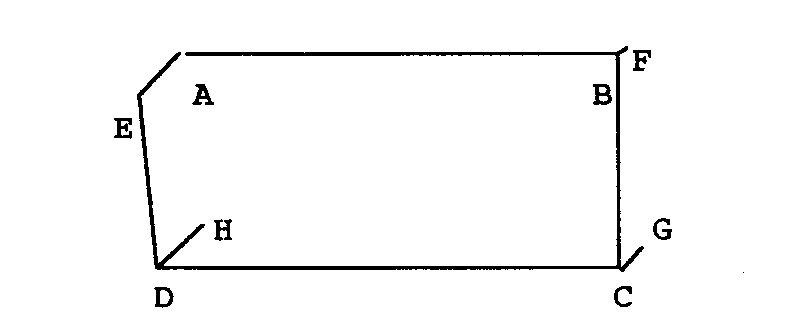
The above is the diagram of a simple close, AB, BC, CD and DE represent the raw traverse. EA represents the misclose vector.
I will define an unadjusted area as being the figure ABCDEA. The Bowditch adjusted figure is defined by AFGHA.
It can easily be seen that the Bowditch adjusted area is as shown below
adjusted area = ABCDEA + AFBA + BFGCB + CGHDC + DHAED
I have tried to write this in a general sense. In reality the first two corrections will be positive and the last two will be negative. As to whether they are positive or negative depends on the direction of the misclose vector.
Now let Vector AB = Li and length = li
Also let Vector BC = L2 and length = l2
Also let Vector CD = L3 and length = l3
Also let Vector DE = L4 and length = l4
Let the misclose vector divided by the perimiter = M
Let the adjustment vectors be as shown below
BF = Q1, CG = Q2, DH = Q3 & EA = Q4
It can also be shown that the area BFGCB = L2@( Q2 + Q3 )
2
Then if we sum all the partial areas for adjustment we finally get the total adjustment needed.
[Sum of ( { twice Sum of all Is up to In } + In +1 ) Ln+1 ] @H
2
In the above context n ranges from 0 to 4. L0 being zero length.
The above notation is a bit unusual. Would have liked to have used the greek sigma notation, however there is no guarantee that the greek letters will come out the same on all computers.
Again the above is simply to apply. Easier to use than Spencer Broughton's original algorithm. ( His algorithm is probably used by thousands of Surveyors daily; yet few would realise that they are using it.)
Well that finishs off this tutorial. There are probably many more simply application of vectors to ordinary Surveying. let me know if find some new ones. I will add any new ones to this tutorial and acknowledge your contribution.
[